فعالیت
2- چاپخانهای میخواهد ۲۸۲ جلد کتاب را صحافی کند. اگر مدیر این چاپخانه بخواهد این تعداد کتاب را بین ۳ نفر کارگر چاپخانه به طور مساوی تقسیم کند آیا کتابی باقی میماند؟
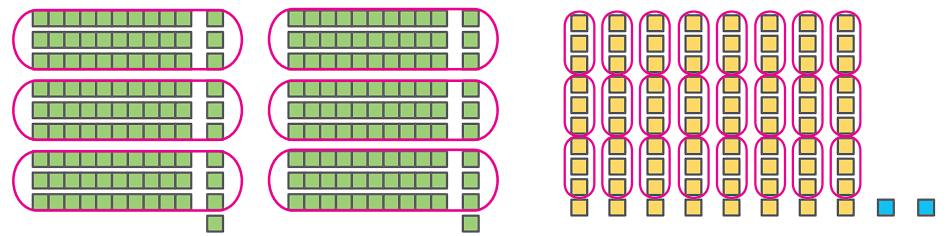
۲۸۲ یعنی ۲ صدتایی، ۸ دهتایی و ۲ تا یکی
با توجّه به شکل، در تقسیم صدتاییها به سه قسمت مساوی چند کتاب باقی میماند؟
در تقسیم دهتاییها چطور؟
همهی کتابها به سه قسمت مساوی تقسیم شدهاند به غیر از:
چه ارتباطی بین $۲+۸+۲$ و رقمهای عدد ۲۸۲ وجود دارد؟
– آیا میتوانید روشی ساده برای تعیین بخشپذیری عدد ۲۸۲ بر ۳ پیشنهاد کنید؟
آیا در تقسیم کتابها بین ۳ نفر برای صحافی، کتابی باقی میماند؟
۲۸۲ یعنی ۲ صدتایی، ۸ دهتایی و ۲ تا یکی
با توجّه به شکل، در تقسیم صدتاییها به سه قسمت مساوی چند کتاب باقی میماند؟
در تقسیم دهتاییها چطور؟
همهی کتابها به سه قسمت مساوی تقسیم شدهاند به غیر از:
چه ارتباطی بین $۲+۸+۲$ و رقمهای عدد ۲۸۲ وجود دارد؟
– آیا میتوانید روشی ساده برای تعیین بخشپذیری عدد ۲۸۲ بر ۳ پیشنهاد کنید؟
آیا در تقسیم کتابها بین ۳ نفر برای صحافی، کتابی باقی میماند؟
با توجّه به شکل، در تقسیم صدتاییها به سه قسمت مساوی ۲ کتاب باقی میماند.
در تقسیم دهتاییها ۸ کتاب باقی میماند.
ارتباط بین $۲+۸+۲$ و رقمهای عدد ۲۸۲: $۲+۸+۲$ همان مجموع رقمهای ۲۸۲ است.
روشی ساده برای تعیین بخشپذیری عدد ۲۸۲ بر ۳: میتوانیم رقمهای عدد ۲۸۲ را با هم جمع کنیم و مجموع آنها را بر ۳ تقسیم کنیم.
$۲+۸+۲=۱۲$
چون جمع رقمهای عدد ۲۸۲ بر ۳ بخشپذیر است، پس عدد ۲۸۲ نیز بر ۳ بخشپذیر است.
در تقسیم کتابها بین ۳ نفر برای صحافی، کتابی باقی نمیماند.
در تقسیم دهتاییها ۸ کتاب باقی میماند.
ارتباط بین $۲+۸+۲$ و رقمهای عدد ۲۸۲: $۲+۸+۲$ همان مجموع رقمهای ۲۸۲ است.
روشی ساده برای تعیین بخشپذیری عدد ۲۸۲ بر ۳: میتوانیم رقمهای عدد ۲۸۲ را با هم جمع کنیم و مجموع آنها را بر ۳ تقسیم کنیم.
$۲+۸+۲=۱۲$
چون جمع رقمهای عدد ۲۸۲ بر ۳ بخشپذیر است، پس عدد ۲۸۲ نیز بر ۳ بخشپذیر است.
در تقسیم کتابها بین ۳ نفر برای صحافی، کتابی باقی نمیماند.
⭐ مسیر ستارهها در حل مسئله ⭐
عددی بر ۳ بخشپذیر است که جمع رقمهایش بر ۳ بخشپذیر باشد.
اگر پس از صحافی برای حمل آسان کتابها، بخواهند آنها را به طور مساوی در ۹ کارتن قرار دهند، آیا کتابی باقی میماند؟
با توجّه به فعّالیت ۱، از تقسیم صدتاییها به ۹ قسمت مساوی ۲ و از تقسیم دهتاییها به ۹ قسمت مساوی ۸ باقی میماند.
بنابراین همهی کتابها به طور مساوی بین ۹ کارتن تقسیم میشوند به غیر از :
۲: باقیماندهی تقسیم صدتاییها بر ۲
۸: باقیماندهی تقسیم دهتاییها بر ۹
۲: یکی
$۱۲= 2+۸+۲$
که اگر ۱۲ را بر ۹ تقسیم کنیم، باقیمانده ۳ میشود. پس ۳ کتاب باقی میماند.
آیا از روشی که برای تعیین بخشپذیری اعداد بر ۳ گفته شد، برای تعیین بخشپذیری بر ۹ نیز میتوان استفاده کرد؟
با توجّه به فعّالیت ۱، از تقسیم صدتاییها به ۹ قسمت مساوی ۲ و از تقسیم دهتاییها به ۹ قسمت مساوی ۸ باقی میماند.
بنابراین همهی کتابها به طور مساوی بین ۹ کارتن تقسیم میشوند به غیر از :
۲: باقیماندهی تقسیم صدتاییها بر ۲
۸: باقیماندهی تقسیم دهتاییها بر ۹
۲: یکی
$۱۲= 2+۸+۲$
که اگر ۱۲ را بر ۹ تقسیم کنیم، باقیمانده ۳ میشود. پس ۳ کتاب باقی میماند.
آیا از روشی که برای تعیین بخشپذیری اعداد بر ۳ گفته شد، برای تعیین بخشپذیری بر ۹ نیز میتوان استفاده کرد؟
بله، $۳$ کتاب باقی میماند.
از روش بخشپذیری بر $۳$ برای تعیین بخشپذیری بر $۹$ هم میتوان استفاده کرد، با این تفاوت که مجموع ارقام باید بر $۹$ بخشپذیر باشد.
⭐ مسیر ستارهها در حل مسئله ⭐
عددی بر ۹ بخشپذیر است که جمع رقمهایش بر ۹ بخشپذیر باشد.

پرسش و پاسخ بدون پرسش
تا کتون پرسشی ثبت نشده.